Turning up the heat on Earth temperature modelling — AuScope
Modelling temperature in the Earth’s crust is accomplished by populating a geological model with thermal properties, such as thermal conductivity and rates of heat production, and solving a numerical model of thermal diffusion with assigned boundary conditions.
The desired temperature solution is often the one that best matches our observations — e.g. temperature in a well — but strong assumptions are made of how thermal properties vary with depth, which result in simple first-order predictions of the temperature field.
Posing an inverse problem is a way to ascertain how much your observations tells you about a particular model. Finding better and better solutions usually require running model after model with slight changes in the input parameters to find a better fit to the observations.
For instance, a lower rate of heat production in one layer of the Earth’s crust may result in a better match to an observation of heat flow coming out of the ground. This is fine if the number of unknowns is small, but when we start to increase the quantity of unknown parameters then it takes an exponentially long time to find the model that best reproduces our observations.
In our recent paper with Prof Peter Rayner of the University of Melbourne accepted in Geophysical Journal International, we formulate a novel inversion method that uses the gradient to quickly find the optimal configuration of thermal properties that best match our observations.

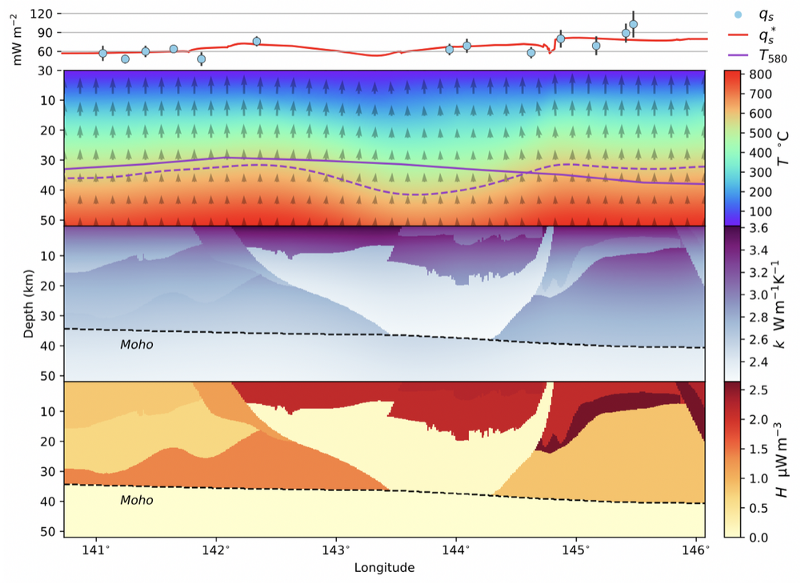
We publish improved estimates of the thermal state of the crust in Victoria using heat flow measurements and Curie depth in a joint inversion using 3D geological models, and numerical models of thermal diffusion. The outcome of this work is an estimation of basal heat flux, thermal properties, and the rate of heat production for various domains in the model together with uncertainty information.
Originally published at https://www.auscope.org.au on September 12, 2019.